Analisis Regresi Ganda menggunakan SPSS

Pengantar

Regresi ganda adalah perluasan dari regresi linier sederhana. Analisis regresi ganda digunakan apabila kita bermaksud memprediksi nilai suatu variabel berdasar nilai dari dua atau lebih variabel lainnya. Variabel yang nilainya kita prediksi disebut variabel terikat (kadang disebut variabel bergantung, variabel dependen, variabel hasil, variabel kriteria, atau variabel target). Variabel yang kita gunakan untuk memprediksi nilai variabel terikat disebut variabel bebas (atau kadang-kadang disebut prediktor, variabel penjelas/explanatory, ata variabel regresor).

Misalnya, kita dapat menggunakan regresi ganda untuk memahami apakah nilai ujian dipengaruhi oleh lamanya waktu belajar, kecemasan, kehadiran dosen dalam perkuliahan, dan jenis kelamin. Kita juga dapat menggunakan regresi ganda untuk memahami apakah konsumsi rokok harian dapat diprediksi berdasarkan durasi merokok, umur mulai merokok, jenis perokok, pendapatan, dan jenis kelamin.

Regresi ganda juga memungkinkan kita menentukan mencocokkan model dan sumbangan/kontribusi relatif masing-masing prediktor. Misalnya,  mungkin kita ingin mengetahui berapa banyak variasi dalam nilai ujian dapat dijelaskan oleh lamanya waktu belajar, kecemasan, kehadiran dosen, dan jenis kelamin mahasiswa, tetapi juga “sumbangan relatif” masing-masing variabel bebas dalam menjelaskan varians.

Panduan ini menunjukkan pada Anda bagaimana melakukan analisis regresi ganda menggunakan SPSS, menginterpretasi dan melaporkan hasilnya. Sebelum itu, perlu dipahami mengenai asumsi-asumsi yang harus dipenuhi oleh data agar analisis regresi memberikan hasil yang valid.

Asumsi

Bila Anda memilih menganalisis data Anda dengan regresi ganda, sebagian dari proses analisis adalah untuk memastikan bahwa data yang akan Anda analisis memang boleh dianalisis menggunakan regresi ganda. Anda perlu melalui tahapan ini karena kita hanya dapat menggunakan regresi ganda apabila data yang dianalisis memenuhi 8 asumsi yang diperlukan agar hasil analisisnya valid. Dengan SPSS, uji asumsi itu dapat dilakukan hanya dengan melakukan beberapa klik tombol. 

Bukan hal yang mengejutkan apabila data yang Anda peroleh tidak bisa memenuhi satu atau lebih syarat atau asumsi. Meskipun demikian, tidak perlu khawatir. Meski data yang Anda peroleh tidak memenuhi asumsi tertentu, selalu ada jalan keluar.

Delapan asumsi yang diperlukan untuk melakukan analisis regresi ganda adalah:

• Asumsi #1: Vaiabel terikat harus diukur dengan skala kontinyu yakni merupakan variabel interval atau ratio). Contoh variabel yang memenuhi kriteria ini adalah waktu belajar (diukur dalam jam), kecerdasan (diukur menggunakan skor IQ), nilai ujian (diukur dengan angka 0 sampai 100), bobot atau berat badan (diukur dalam kg), dan sebagainya.
• Asumsi #2: Anda memiliki dua atau lebih variabel bebas, yang merupakan variabel kontinyu (misalnya, variabel interval atau ratio) atau kategori (misalnya, variabel ordinal atau nominal). Sebagai contoh variabel kontinyu, lihat penjelasan sebelumnya. Contoh variabel ordinal meliputi skala Likert (misalnya skala 7-poin dari sangat setuju sampai sangat tidak setuju), perangkingan (misalnya, skala 3-poin  menjelaskan tingkat ketertarikan konsumen pada produk tertentu, mulai dari "tidak tertarik",  "cukup tertarik", sampai "sangat tertarikt"). Contoh variabel nominal misalnya jenis kelamin (pria dan wanita), etnis (misalnya: Kaukasoid, Afro-Amerika dan Hispanik), tingkat aktivitas fisik (misalnya, 4 kelompok: diam, aktivitas rendah, aktivitas sedang dan aktivitas tinggi), profesi paramedis (misalnya 5 kelompok: ahli bedah, dokter umum, perawat, dokter gigi, terapis), dan sebagainya.
• Asumsi #3: Harus memiliki independensi observasi atau independence of observations (yakni independence of residuals), yang dapat diperiksa dengan mudah menggunakan statistika Durbin-Watson, yang dapat dilakukan dengan SPSS. Akan dijelaskan bagaimana menginterpretasi hasil statistika Durbin-Watson.
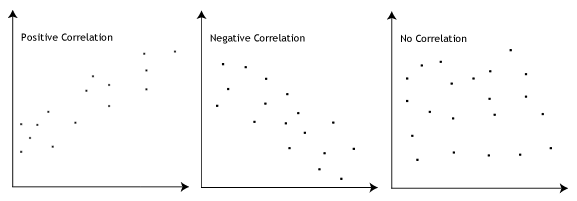
• Asumsi #4: Harus ada hubungan linier antara  (a) variabel terikat dengan masing-masing variabel bebas, dan (b) variabel terikat dengan vaiabel bebas secara kolektif. Ada beberapa cara untuk menguji linieritas hubungan, diantaranya dengan membuat scatterplots dan partial regression plots menggunakan SPSS, dan kemudian secara visual memeriksa kelinieran scatter plot atau partial regession plot tersebut. Jika hubungannya tidak linier, Anda harus mempertimbangkan untuk menggunakan analisis regresi  non-linier atau melakukan transformasi data Anda.
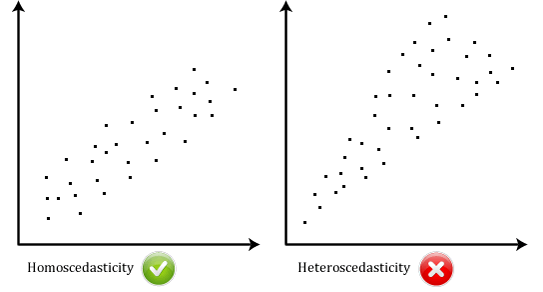
• Asumsi #5: Data Anda harus memenuhi syarat homoskedastisitas, yang cirinya adalah varians sepanjang garis-cocok (line of best fit) tetap sama. Ketika Anda menganalisis data Anda, Anda perlu membuat plot studentized residuals terhadap unstandardized predicted values. 
• Asumsi #6: Data Anda harus menunjukkan multikolineritas, yang terjadi bila Anda memiliki dua atau lebih variabel bebas yang berkorelasi tinggi satu sama lain. Ini akan menimbulkan masalah dalam memahami variabel bebas manakah yang berkontribusi kepada varians yang dijelaskan dalam variabel terikat. 
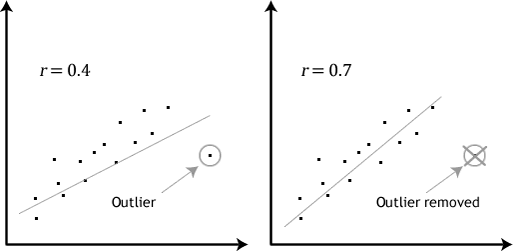
• Asumsi #7: Harus tidak ada outlier (kadang disebut high leverage points, atau highly inflential points).  Outliers, leverage dan influential point adalah istilah-istilah  yang menggambarkan pengamatan terhadap data yang tampak tidak biasa. Masing-masing ketidakbiasaan itu memiliki dampak yang berbeda terhadap garis regresi. Data-data tidak biasa tersebut memiliki efek negatif terhadap persamaan regresi yang dihasilkan, padahal persamaan regresi merupakan alat utama untuk memprediksi nilai variabel terikat berdasar nilai-nilai pada variabel bebas. 
• Asumsi #8: Terakhir, Anda perlu memeriksa bahwa  residuals (errors) kira-kira berdistribusi normal. Dua metode umum untuk memeriksa asumsi ini adalah menggunakan  (a) histogram (yang digambar berimpitan dengan kurva normal) dab Normal P-P Plot; atau (b) a Normal Q-Q Plot dari  studentized residuals. 

Anda dapat menguji asumsi  #3, #4, #5, #6, #7 dan #8 menggunakan SPSS. Asumsi #1 dan #2 harus diperiksa terlebih dahulu sebelum memeriksa asumsi #3, #4, #5, #6, #7 dan #8. Perlu diingat bahwa bila asumsi-asumsi tidak dipenuhi akan berakibat pada tidak validnya hasil analisis.

Contoh soal dan penyelesaian untuk regresi ganda silahkan unduh pada file berikut ini.

Analisis Regresi Linier dengan SPSS

Pendahuluan

Regresi linier adalah langkah lanjut setelah korelasi. Analisis ini digunakan bila kita ingin memprediksi nilai suatu variabel berdasar pada nilai variabel lainnya. Variabel yang ingin kita prediksi nilainya disebut sebagi variabel terikat atau variabel bergantung (kadang-kadang disebut juga variabel outcome atau variabel capaian).  Variabel yang kita gunakan untuk memprediksi nilai variabel lain disebut variabel bebas (variabel independen, atau juga disebut sebagai variabel prediktor). Misalnya, kita dapat menggunakan regresi linier untuk memmahami apakah kinerja/nilai ujian dapat diprediksi berdasarkan banyaknya waktu yang tersedia untuk ujian atau panjang waktu jeda antara akhir semester dengan saat ujian, atau apakah konsumsi rokok dapat diprediksi berdasar pada durasi waktu merokok, dan sebagainya. Jika kita memiliki dua atau lebih variabel bebas, kita perlu menggunakan regresi ganda (multiple regression).

Untuk mulai menggunakan analisisi regresi, kita perlu memahami asumsi-asumsi yang harus dipenuhi oleh data agar regresi linier memberikan hasil yang valid atau dapat dipercaya.

Asumsi

Jika Anda memilih menganalisis data dengan menggunakan regresi linier, bagian dari proses itu meliputi pemeriksaan untuk memastikan data yang ingin Anda analisis benar-benar dapat dianalisis dengan menggunakan regresi linier. Anda perlu melakukan ini karena analisis regresi hanya tepat digunakan bila data yang Anda miliki lulus 6 persyaratan atau asumsi yang diperlukan untuk regresi linier agar dapat memberikan hasil yang valid. Dalam praktiknya, menguji 6 asumsi hanya menambah sedikit waktu saja, hanya beberapa kali klik tombol-tombol kerja SPSS, sama sekali bukan merupakan langkah yang sulit.

 
Asumsi #1

Kedua variabel yang akan Anda analisis harus merupakan variabel yang berskala atau berlevel interval atau  rasio (artinya, keduanya merupakan variabel kontinyu. Misalnya, waktu atau lamanya waktu libur menjelang ujian (diukur dalam satuan jam), inteligensi (diukur dengan skor IQ), kinerja atau skor ujian (diukur dengan nilai 0 – 100), bobot (diukur dalam kilogram), dan sebagainya.

 
Asumsi #2

Asumsi kedua adalah hubungan kedua variabel adalah hubungan yang linier. Ada banyak cara untuk memeriksa apakan hubungan kedua variabel linier atau tidak, meskipun demikian, dalam handout ini disarankan membuat scatterplot menggunakan SPSS. Scatterplot ayau plot sebaran dapat digunakan untuk memeriksa linieritas. Scatterplot data Anda mungkin terlihat seperti gambar berikut ini:

Jika hubungan yang ditunjukkan oleh scatterplot tidak linier, Anda harus menjalankan regresi non-linier atau melakukan transformasi terhadap data tersebut, yang bisa juga Anda lakukan dengan SPSS. Pada langkah lanjut nanti, akan ditunjukkan bagaimana : (a) membuat scatterplot untuk memeriksa linieritas bila akan melakukan regresi linier dengan SPSS, (b) menginterpretasi hasil scatterplot yang berbeda, dan (c) melakukan transformasi data menggunakan SPSS apabila tidak ada hubungan linier di antara dua variabel.

 
Asumsi #3

Harus tidak ada data pencilan (outlier) yang signifikan. Pencilan adalah satu data di dalam kelompok data yang tidak mengikuti pola yang umum. Misalnya, dalam studi mengenai skor IQ mahasiswa, dengan populasi 100 mahasiswa diperoleh rerata skor 108 dengan hanya variasi kecil antar mahasiswa, satu mahasiswa memiliki skor IQ=156, artinya sangat tidak biasa. Scatterplot berikut ini menunjukkan dampak potensial dari data pencilan.

Masalah yang ditimbulkan oleh data pencilan adalah adanya efek negatif pada persamaan regresi yang digunakan untuk memprediksi nilai variabel terikat atau variabel bergantung berdasar nilai variabel bebas (atau prediktor). Data pencilan ini akan mengubah keluaran yang dihasilkan SPSS dan mengurangi akurasi prediksi pada data Anda. Untungnya, bila menggunakan SPSS untuk menghitung regresi linier terhadap data Anda, dengan mudah Anda bisa memasukkan kriteria untuk membantu mendeteksi adanya data pencilan. Pada panduan lanjut mengenai regresi linier akan ditunjukkan (a) bagaimana mendeteksi data pencilan menggunakan “casewise diagnostics”, yang merupakan proses sederhana bila menggunakan SPSS, dan (b) mendiskusikan beberapa opsi yang Anda miliki untuk menangani data pencilan.

 
Asumsi #4

Anda harus memiliki independensi observasi, yang dengan mudah dapat diperiksa dengan statistika Durbin-Watson, yang merupakan tes sederhana untuk dilakkan dengan SPSS. Akan dijelaskan bagaimana memaknai hasil statistika Durbin-Watson dalam panduan lanjur menggunakan analisis regresi.

 
Asumsi #5

Data yang Anda miliki harus menunjukkan homokedastisitas (homocedasticity), yakni varians-varians sepanjang garis regresi terbaiknya tetap sama sepanjang garis. Perhatikan dua scatterplot berikut ini untuk memahami homokedastisitas. Data pada plot kiri adalah data yang memenuhi syarat homokedastisitas, sedangkan yang kanan tidak.

Saat menganalisis data Anda, akan sangat beruntung apabila scatterplotnya menyerupai salah satu dari gambar di atas. Data yang sebenarnya seringkali lebih berantakan. Meskipun demikian, dalam panduan lanjut akan dijelaskan: (a) beberapa hal yang perlu diperhatikan dalam memaknai data, dan (b) cara yang memungkinkan untuk melanjutkan analisis apabila data yang Anda miliki tidak memenuhi persyaratan di atas.

 
Asumsi #6

Terakhir, Anda perlu memeriksa bahwa residu (galat) pada kedua variabel yang dianalisis mendekati distribusi normal (masalah ini akan dijelaskan pada panduan lanjutnya). Dua metode yang berbeda untuk memeriksa asumsi ini termasuk di dalamnya menggunakan histogram (yang ditumpangtindihkan pada kurve normal) atau dengan menggunakan Normal P-P Plot. Dalam panduan lanjut akan ditunjukkan (a) bagaimana cara memeriksa asumsi ini dengan menggunakan SPSS, baik dengan cara menggunakan histogram yang ditumpangtindih dengan kurve normal atau dengan Normal P-P Plot, (b) penjelasan cara memaknai diagram tersebut, dan (c) memberikan solusi yang mungkin jika data Anda tidak memenuhi asumsi ini.

Anda dapat memeriksa asumsi #2, #3, #4, #5 dan #6 menggunakan SPSS. Asumsi #2 dan #3 harus diperiksa lebih dahulu sebelum memeriksa asumsi #4, #5, dan #6. Disarankan menguji asumsi-asumsi ini secara berurutan karena jika ada pemaksaan terhadap asumsi yang tidak dapat diperbaiki lagi, Anda tidak dapat lagi menggunakan regresi linier tunggal ini (meskipun Anda mungkin bisa melakukan analisis statistik lainnya).  Juga, periksa asumsi #4, #5, dan #6 pada saat bersamaan dengan prosedur regresi linier dalam SPSS, sehingga lebih mudah menangani ini setelah memeriksa asumsi #2 dan #3. Hanya perlu diingat bahwa jika Anda tidak menganalisis tanpa memenuhi asusmsi-asumsi tersebut, hasil yang Anda dapatkan tidak akan valid.  

Contoh analisis regresi sederhana dapat diunduh dari tautan berikut ini.